策略梯度
说明
Q-learning, Sarsa, DQN都是value-based的强化学习方法, 首先学习到价值函数,然后根据价值函数选择动作.
考虑到Exploration-expolitation(探索与利用)的问题. 一般是采用 $\epsilon$-greedy 的方式选择动作.
输出的动作都是”硬”选择. 本章将讲述另外一类算法, policy-based(基于策略)的强化学习方法.
- 输入为状态,输出为各种动作的概率. 软选择
- 目标是奖励的期望最大化.
- 手段是不断调整策略模型的参数 $\theta$
策略梯度方法的优缺点
优点
- 保证局部收敛
- 适用于高位动作空间或者是连续动作空间, 或者是用于难于计算 $arg\max_a Q(s,a)$ 的情况.
- 能学习到随机策略.
- 在玩剪刀,石头,布之类的游戏时, 任何确定性策略都不是好策略
- 在环境状态不能完全被观测时, 从观测上来说一样结果的实际情况可能是两个或多个不同的状态(状态观测不完全导致不能分辨不同状态), 此时也需要随机策略, 也就是给定状态,执行的动作具有随机性.
- 很多情况下, 比基于学习Q或者V价值函数的方法简单一些. 比如当小球从从空中某个位置落下你需要左右移动接住时,计算小球在某一个位置时采取什么行为的价值是很难得;但是基于策略就简单许多,你只需要朝着小球落地的方向移动修改策略就行。
缺点
- Less sample efficient
- 只能保证局部收敛,而不是全局收敛
策略优化目标
我们优化策略的最终目的是什么?尽可能获得更多的奖励。我们设计一个目标函数来衡量策略的好坏,针对不同的问题类*型,这里有三个目标函数可以选择:
- Start value:在能够产生完整Episode的环境下,也就是在个体可以到达终止状态时,我们可以用这样一个值来衡量整个策略的优劣:从某状态s1算起知道终止状态个体获得的累计奖励。这个值称为start value. 这个数值的意思是说:如果个体总是从某个状态s1开始,或者以一定的概率分布从s1开始,那么从该状态开始到Episode结束个体将会得到怎样的最终奖励。这个时候算法真正关心的是:找到一个策略,当把个体放在这个状态s1让它执行当前的策略,能够获得start value的奖励。这样我们的目标就变成最大化这个start value:
Average Value:对于连续环境条件,不存在一个开始状态,这个时候可以使用 average value。意思是 考虑我们个体在某时刻处在某状态下的概率,也就是个体在该时刻的状态分布,针对每个可能的状态计算从该时刻开始一直持续与环境交互下去能够得到的奖励,按该时刻各状态的概率分布求和:
注, $d^{\pi_\theta}(s)$ 是在当前策略下马尔科夫链的关于状态的一个静态分布.- Average reward per time-step:又或者我们可以使用每一个时间步长在各种情况下所能得到的平均奖励,也就是说在一个确定的时间步长里,查看个体出于所有状态的可能性,然后每一种状态下采取所有行为能够得到的即时奖励,所有奖励按概率求和得到:
另外一个策略目标的写法, 这个写法的展开后等于 Average reward per time-step, 不过是强调了调整策略模型参数 $\theta$ 来优化
关于这个写法, 要记住
- $d^{\pi_\theta}(s)$ 在给定策略下,不同状态的分布
- $\pi_\theta(s,a)$ 是给定策略下, 在状态s时不同动作a的概率分布,
- $R(s_t, a_t)$ 是t步时给定状态和动作的奖励.
策略梯度方法
有限差分策略梯度Finite difference Policy Gradient
这是非常常用的数值计算方法,特别是当梯度函数本身很难得到的时候。具体做法是,针对参数θ的每一个分量 $θ_k$,使用如下的公式粗略计算梯度
$u_k$ 是一个单位向量,仅在第k个维度上值为1,其余维度为0. i.e. one-hot向量
有限差分法简单,不要求策略函数可微分,适用于任意策略;但有噪声,且大多数时候不高效. 也能解决问题.
蒙特卡罗策略梯度 Monte-Carlo Policy Gradient
似然比方法, likelihood ratio method
- 定义回合(trajectory) $\tau$ 为状态和动作序列 $s_0, a_0, s_1, …, s_T, a_T$ 并有奖励 $R(\tau) = \sum_{t=0}^T R(s_t, a_t)$
- 定义奖励的期望 $J(\theta) = E[\sum_{t=0}^T R(s_t, a_t); \pi_\theta] = \sum_\tau P(\tau; \theta)R(\tau)$ 可以看出定义就是给定策略参数下,不同回合序列出现的概率乘以序列的奖励. 同时也可以理解如果某种回合(状态和动作序列)的奖励大, 则要调整参数使这种序列出现的概率大.
- 目标, 找到参数 $\theta$ 以最大化下列式子
似然比方法公式推导, 需要梯度上升, 也就是要给出优化目标的梯度函数
- 在等式中,我们假设可以考虑所有的各种组合的回合(也就是所有可能的状态动作序列组合), 现实中基本是做不到的. 近似的做法是采用策略 $\pi_\theta$ 采样出m个回合. 于是等式被近似为
- 从上式中可以看出,我们从概率求期望被近似为采样m个回合求平均. 一个好的副作用就是概率P也被从公式中移除.
为什么叫做似然比方法
个人理解
- 似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性. 概率用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而似然性则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计.
- $L(\theta \vert x_1, x_2, …, x_n) = P_\theta(x_1, x_2, …, x_n)$ 给定样本,概率分布参数的似然性为给定参数该特定样本出现的概率.
- 常用的最大似然估计方法就是, 写出概率分布并代入样本数据, 然后取对数, 并分别对不同参数求导后设为0, 取得参数的估计.
- 似然比,给定样本数据, 对不同参数的似然性比值关系
- 这里利用梯度提升,更新前后的参数对应不同的似然性, 似然性的取对数的差值关系对应为原似然性的比值关系.
分解回合为状态和动作序列
- 第一步分解很简单, 回合出现的概率为, 根据策略计算时刻t时的状态下采取各动作的概率 $\pi_\theta (a_t \vert s_t)$ 和时刻t时,状态s与动作a组合后下一个状态的的概率分布 $P(s_{t+1} \vert s_t, a_t)$
- 第一项中不含有参数 $\theta$, 求导后为0, 同时可以看出优化目标的梯度仅与策略相关,与模型无关
- 分解后结果代回原式
- m个回合的近似估计是无偏估计, 当m趋于无穷时,估计的梯度趋于真实的梯度.
- 最后一个式子也是REINFORCE算法的基础.
softmax 策略
如前所述, $\pi_\theta (a_t \vert s_t)$ 为状态到动作的概率分布函数, 当动作为离散动作时, Softmax函数(或者是最后一层为softmax的神经网络)常被用来表示各动作的概率.
- 我们把行为看成是多个特征在一定权重下的线性代数和:
- 采取某一具体行为的概率与e的该值次幂成正比, (去掉了归一化因子)
- softmax 策略下的计分函数, (把归一化因子又放回来了)
高斯策略
略过
REINFORCE算法
策略梯度中学习的第一个算法.
- 初始化策略的参数$\theta$ (例如很小的随机数)
- 执行策略 $a_t \sim \pi(s_t)$ 从策略函数(是给定状态下动作的概率分布)中采样出动作, 记录 状态,动作和奖励. $s_0, a_0, r_0, s_1, a_1, r_1,…,s_T,a_T,r_T$
- 计算整个回合的返回 $R=\sum_{t=0}^T r_t$
- 计算策略梯度
- 更新参数
- 重复步骤2到5直至收敛
Cart Pole
Cart Pole在OpenAI的gym模拟器里面,是相对比较简单的一个游戏。游戏里面有一个小车,上有竖着一根杆子。小车需要左右移动来保持杆子竖直。如果杆子倾斜的角度大于15°,那么游戏结束。小车也不能移动出一个范围(中间到两边各2.4个单位长度)。如下图所示:

- 状态: 水平位移, 水平位移速度, 杆子倾斜角度, 杆子倾斜角度的速度
- 动作: 离散动作, 力的大小是固定的, 只是可以选择施加力的方向
- 奖励: 每步奖励为1
- 终止条件: 杆子倾斜的角度大于15° (失败), 小车移动出范围(失败), 走了200步(成功)
REINFORCE的更新
这是一个实现上的问题, 在监督学习的训练中, 我们有标签数据, 正确的标签数据与我们估计值之间的某种形式的误差为代价函数是我们的优化目标, 我们求梯度然后采用梯度下降的方式进行模型参数更新.
这里,
- 我们有一个根据策略给出的动作概率分布后的采样动作
- 我们没有正确的标签,我们只有执行采样出的动作后得到的反馈奖励
我们采用伪标签的方式
- 由于后续的反馈奖励R都是由采样后的样本动作a而得来的,所以伪标签的值应当设为采样后的动作.
- 所以对数似然函数的梯度的方向就是朝着采样后得到的动作的方向, 如果采样后动作得到的反馈奖励比较小或者负数,则相应的参数更新量也比较小或者是负的, 如果采样后动作得到的反馈奖励比较大, 则相应的参数更新量也会比较大. 从累积参数更新来说,参数的更新会增大反馈奖励大的动作概率.
总结, 采用伪标签, 我们总是尝试使采样出的动作在将来更有可能发生, 但是反馈奖励大的动作我们增大的更多(参数更新量经过R的缩放), 而反馈奖励小的动作我们增大的小一些, 由于概率分布的归一化, 反馈奖励小的动作实际上我们是减小了发生的概率.
同时从这里也可以看出一个潜在的改进, 就是反馈奖励小的动作(例如反馈奖励小于平均反馈奖励的)应当是负梯度,反馈奖励大的动作(例如反馈奖励大于平均反馈奖励的)是正梯度. 这其实是其改进算法REINFORCE BASELINE方法的基础.
降低方差来改进REINFORCE算法
偏差与方差 bias and variance
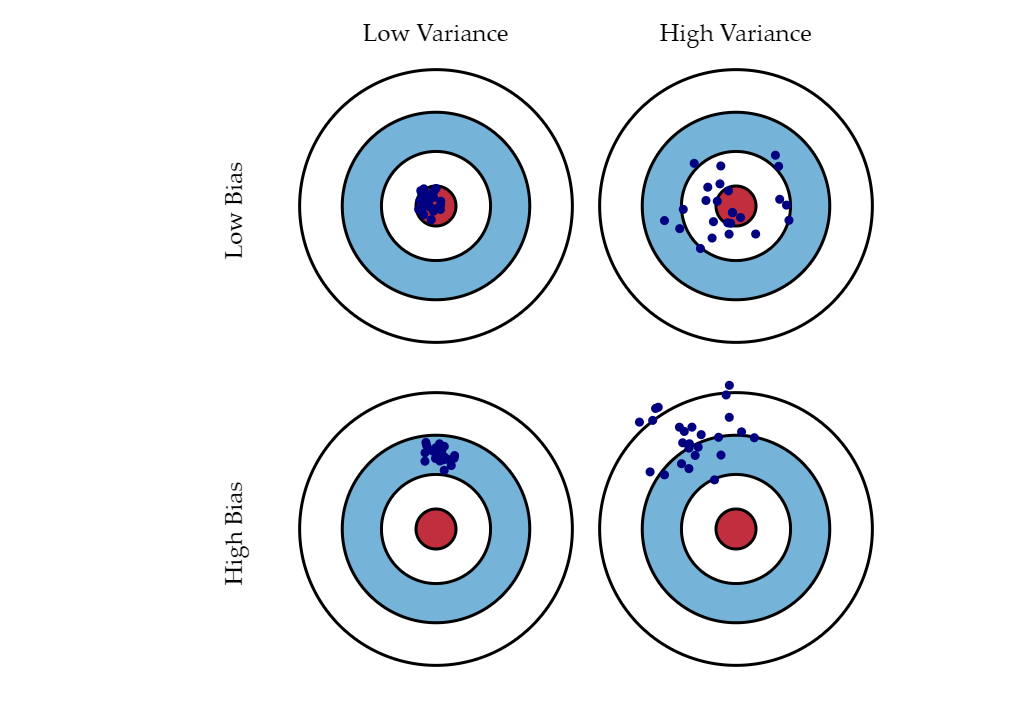
引用网页 http://scott.fortmann-roe.com/docs/BiasVariance.html
REINFORCE用到无偏估计, 应该是低偏差的情况, 所以我们需要降低方差来提高性能.
Discounted Return
出发点, 在基础的REINFORCE算法中,我们对于回合中每一步的奖励都是一致的, 也就是回合的总奖励.
- 如果回合中有些好的行为,也有坏的行为, 最后的奖励为0, 我们则啥都学不到.
- 如果回合的开始有些坏的行为, 但是后续有很多好的行为,最后得到了比较好的反馈奖励, 我们则会鼓励所有的行为,包括开始的坏行为,这样学习的效率不高, 方差也大, 有很多坏的行为可能在一些回合中受到了鼓励.
改进, 采用每步打折的奖励(per-step discounted return)
时刻t的奖励R,是使用从时刻t之后的每步的奖励之和,且每步的奖励随时间乘以折扣系数gamma.
REINFORCE with BASELINE
正如小节, REINFORCE的更新中提到的潜在的改进所述,
- 首先, 我们对当前策略建立一个估计,该估计是期望的性能(反馈奖励), 这个估计称为基线(baseline), $b_t = E[r_t; \theta]$
- 在基础的REINFORCE算法中, 我们用反馈奖励对梯度缩放, 而一个改进是明确的指出, 如果策略的行为得到奖励低于策略的期望奖励, 说明这些行为不值得鼓励应该是负梯度, 只有得到反馈奖励高于期望时的行为才值得鼓励.
- 结合discounted return, 梯度公式改写为如下式子.
- 简言之, 采用baseline技术, 即使在回合中得到得到的奖励为正, 只要其奖励低于期望,我们仍然用负梯度来(不鼓励)该回合行为的发生
基线的选择
- 常量 $b=\frac{1}{m} \sum_{i=1}^m R(\tau^i)$
- 依赖与时间的 $b_t = \frac{1}{m} \sum_{i=1}^m \sum_{t^\prime=t}^T r_{t^\prime}^i$
- 基于时间和状态的, $b_t(s_t) = E[\sum_{t^\prime=t}^T r_{t^\prime} \vert s_t]$ .
- 基于时间和状态的基线,实际就是在计算value function.
采用value function作为基线的方案
如何估计 $V_\phi$, 直接的思路如下
- 执行m个回合 $\tau_1, \tau_2, …, \tau_m$ 并记录状态和奖励
- 以最小均方差为代价函数, 用梯度下降来调整参数 $\phi$ 做价值函数的近似.
m个回合, 每个回合T步
具体算法
- 初始化策略的参数 $\theta$ (例如很小的随机数) 和 价值函数的参数 $\phi$
- 对每个回合 1,2,…,n 执行
- 执行当前策略 $a_t \sim \pi(s_t)$ 从策略函数(是给定状态下动作的概率分布)中采样出动作, 记录 状态,动作和奖励. $s_0, a_0, r_0, s_1, a_1, r_1,…,s_T,a_T,r_T$
- 对于每一步计算discounted return $R_t = \sum_{t^\prime=t}^T \gamma^{t^\prime-t} r_{t^\prime}$
- 对所有的每一步,通过最小化均方差 $ \vert V_\phi(s_t) - R_t \vert ^2$ 来重新拟合(refit)基线, 也就是更新value function的参数
- 计算策略梯度
- 更新策略参数
- 重复步骤直至收敛
REINFORCE with baseline 算法实践
代码部分
建立策略神经网络
import cntk as C
from cntk.layers import Sequential, Dense
from cntk.logging import ProgressPrinter
import numpy as np
import gym
...
state_dim = env.observation_space.shape[0] # Dimension of state space
action_count = env.action_space.n # Number of actions
hidden_size = 128 # Number of hidden units
update_frequency = 20
# The policy network maps an observation to a probability of taking action 0 or 1.
observations = C.sequence.input_variable(state_dim, np.float32, name="obs")
W1 = C.parameter(shape=(state_dim, hidden_size), init=C.glorot_uniform(), name="W1")
b1 = C.parameter(shape=hidden_size, name="b1")
layer1 = C.relu(C.times(observations, W1) + b1)
W2 = C.parameter(shape=(hidden_size, action_count), init=C.glorot_uniform(), name="W2")
b2 = C.parameter(shape=action_count, name="b2")
layer2 = C.times(layer1, W2) + b2
output = C.sigmoid(layer2, name="output")
设立标签(label)(后续的代码可以看出是伪标签), 计算discounted reward, 计算损失函数($J(\theta)$), 创建优化器
# Label will tell the network what action it should have taken.
label = C.sequence.input_variable(1, np.float32, name="label")
# return_weight is a scalar containing the discounted return. It will scale the PG loss.
return_weight = C.sequence.input_variable(1, np.float32, name="weight")
# PG Loss
loss = -C.reduce_mean(C.log(C.square(label - output) + 1e-4) * return_weight, axis=0, name='loss')
# Build the optimizer
lr_schedule = C.learning_rate_schedule(lr=0.1, unit=C.UnitType.sample)
m_schedule = C.momentum_schedule(0.99)
vm_schedule = C.momentum_schedule(0.999)
optimizer = C.adam([W1, W2], lr_schedule, momentum=m_schedule, variance_momentum=vm_schedule)
用神经网络做value function的近似, 模型的输出就是估计的价值(也就是基线). 这里称之为评论家(critic).
critic_input = 128 # shape : output dimension of input layer
critic_output = 1 # shape : output dimension of output layer
critic = Sequential([
Dense(critic_input, activation=C.relu, init=C.glorot_uniform()),
Dense(critic_output, activation=None, init=C.glorot_uniform(scale=.01))
])(observations)
# TODO 2: Define target and Squared Error Loss Function, adam optimizier, and trainer for the Critic.
critic_target = C.sequence.input_variable(1, np.float32, name="target")
critic_loss = C.squared_error(critic, critic_target)
critic_lr_schedule = C.learning_rate_schedule(lr=0.1, unit=C.UnitType.sample)
critic_optimizer = C.adam(critic.parameters, critic_lr_schedule, momentum=m_schedule, variance_momentum=vm_schedule)
critic_trainer = C.Trainer(critic, (critic_loss, None), critic_optimizer)
算法主体,
- 执行m和回合,
- 在回合的每步时
- 从策略网络采样得到动作action
- 同时该动作也是策略网络训练用的伪标签
- 在环境中执行动作
- 记录状态,动作和奖励
- 回合结束后,计算回合中每步的discounted reward
- 用回合中每步的状态为输入,discounted reward为标签,进行在线回归拟合,就是更新value funtion的神经网络(critic)参数
- 用critic估计出策略的基线(baseline)
- 回合中实际奖励与基线对比,两者差值用于缩放策略网络的梯度
- 计算策略网络相对于伪标签的梯度,并且上一步的计算结果进行缩放, 然后优化器更新策略网络参数
- 在回合的每步时
...
for episode_number in range(max_number_of_episodes):
states, rewards, labels = [],[],[]
done = False
observation = env.reset()
t = 1
while not done:
state = np.reshape(observation, [1, state_dim]).astype(np.float32)
states.append(state)
# Run the policy network and get an action to take.
prob = output.eval(arguments={observations: state})[0][0][0]
# Sample from the bernoulli output distribution to get a discrete action
action = 1 if np.random.uniform() < prob else 0
# Pseudo labels to encourage the network to increase
# the probability of the chosen action. This label will be used
# in the loss function above.
y = 1 if action == 0 else 0 # a "fake label"
labels.append(y)
# step the environment and get new measurements
observation, reward, done, _ = env.step(action)
reward_sum += float(reward)
# Record reward (has to be done after we call step() to get reward for previous action)
rewards.append(float(reward))
stats.episode_rewards[episode_number] += reward
stats.episode_lengths[episode_number] = t
t += 1
# Stack together all inputs, hidden states, action gradients, and rewards for this episode
epx = np.vstack(states)
epl = np.vstack(labels).astype(np.float32)
epr = np.vstack(rewards).astype(np.float32)
# Compute the discounted reward backwards through time.
discounted_epr = discount_rewards(epr)
# TODO 3
# Train the critic to predict the discounted reward from the observation
# - use train_minibatch() function of the critic_trainer.
# - observations is epx which are the states, and critic_target is discounted_epr
# - then predict the discounted reward using the eval() function of the critic network and assign it to baseline
critic_trainer.train_minibatch({observations:epx, critic_target:discounted_epr}) # modify this
baseline = critic.eval({observations:epx}) # modify this
# Compute the baselined returns: A = R - b(s). Weight the gradients by this value.
baselined_returns = discounted_epr - baseline
# Keep a running estimate over the variance of the discounted rewards (in this case baselined_returns)
for r in baselined_returns:
running_variance.add(r[0])
# Forward pass
arguments = {observations: epx, label: epl, return_weight: baselined_returns}
state, outputs_map = loss.forward(arguments, outputs=loss.outputs,
keep_for_backward=loss.outputs)
# Backward pass
root_gradients = {v: np.ones_like(o) for v, o in outputs_map.items()}
vargrads_map = loss.backward(state, root_gradients, variables=set([W1, W2]))
for var, grad in vargrads_map.items():
gradBuffer[var.name] += grad
# Only update every 20 episodes to reduce noise
if episode_number % update_frequency == 0:
grads = {W1: gradBuffer['W1'].astype(np.float32),
W2: gradBuffer['W2'].astype(np.float32)}
updated = optimizer.update(grads, update_frequency)
# reset the gradBuffer
gradBuffer = dict((var.name, np.zeros(shape=var.shape))
for var in loss.parameters if var.name in ['W1', 'W2', 'b1', 'b2'])
print('Episode: %d/%d. Average reward for episode %f. Variance %f' % (episode_number, max_number_of_episodes, reward_sum / update_frequency, running_variance.get_variance()))
sys.stdout.flush()
reward_sum = 0
stats.episode_running_variance[episode_number] = running_variance.get_variance()
结果比较
Cart Pole游戏的实验
REINFORCE without BASELINE 结果
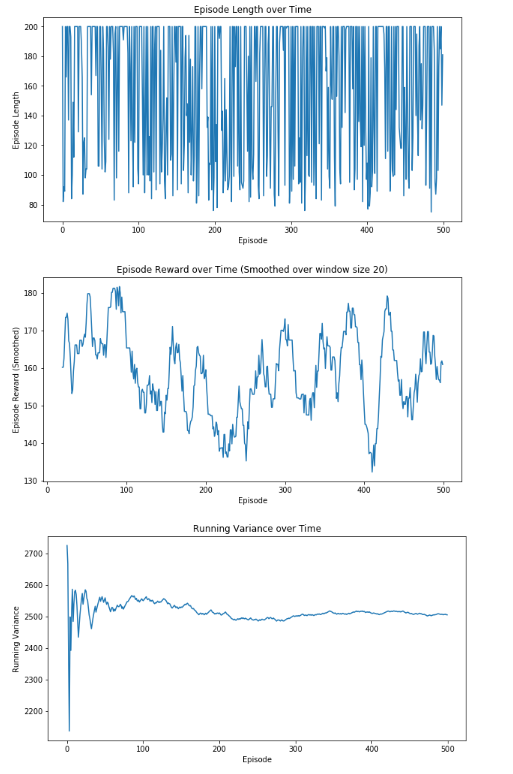
REINFORCE with BASELINE 结果
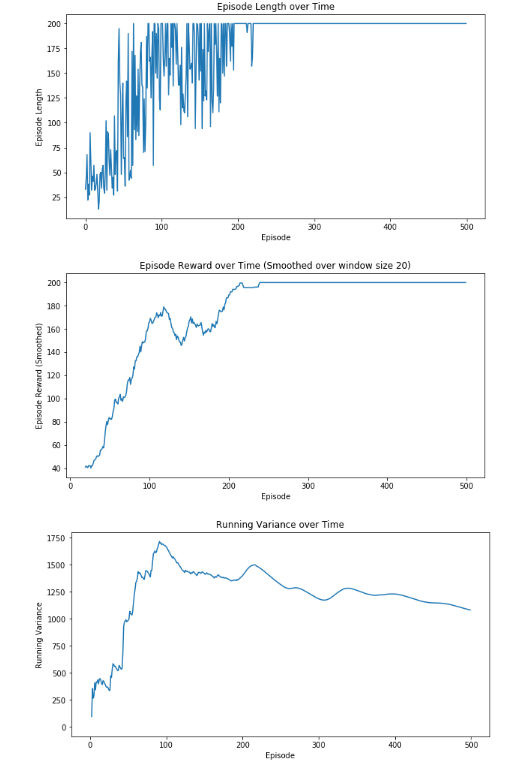
从结果看出, 引入baseline做critic后,方差降低到1200左右,性能稳定了, 240回合左右能稳定输出最大奖励200.
演员-评论家算法
- 包含两个组件
- 演员(actor): 策略部分, 在环境中采取行动
- 评论家(critic): 评估部分, 负责评估选取动作的质量,并给出改进的方向
前面所讲述的带基线的REINFORCE算法也可以说是演员评论家方法
在上面的式子中仍然有一项,我们没有学习,而是用蒙特卡洛方法不断的采样统计的,就是上式中反馈奖励 $R_t$ , 尽管m趋于无穷时是无偏的,但该项具有比较大的方差. 如何降低方差呢,
- 首先回顾Q value function,
- 对比上节中的discounted reward $R_t = \sum_{t^\prime=t}^T \gamma^{t^\prime-t} r_{t^\prime}$ , 两者实质是一样的.
- 改写梯度公式
优势函数 - Advantage function
Q value function 与 V value function的差值为优势函数.
- $V^\pi(s)$ 是在状态s下,服从策略 $\pi$ 所期望的反馈奖励
- $Q^\pi(s,a)$ 是在状态s下,执行动作a, 之后再服从策略pi能得到的期望反馈奖励
- 优势函数advantage告诉我们, 相对于策略 $\pi$ 常规动作a, 特定动作 $a_t$ 能多得到多少反馈奖励.
更新梯度公式为
如何估计A呢? 可以建立一个Q network和一个V network分别估计Q和V然后相减得到A, 但这样会增加bias
N步Q值函数估计, 不用单独的网络来估计Q.
- 利用经验Q值估计, 也就是前面的方法, 特点是低偏差,高方差
- n步Q值估计, 介于纯粹的V值估计和经验估计之间, n步之后是用baseline的V值估计, n步之内是用经验估计, 特点是中偏差,中方差.
- 2步估计, 中偏差,中方差
- 1步估计, 特点是接近baseline的V值估计, 低偏差,高方差
A3C 算法
Asynchronous Advantage Actor Critic算法.
- 采用5步Q值估计计算Advantage的方法
- 在Actor网络和Critic网络之间共享参数
- 同时再多份环境的copy中执行
- 单个环境中的策略是用多个并行环境中所收集的经验数据来累积更新的
- 异步执行的好处是不太需要replay memory.
算法伪代码

n步Q值估计代码
# TODO: Create a function that returns an array of n-step targets, one for each timestep:
# target[t] = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + ... + \gamma^n V(s_{t+n})
# Where r_t is given by episode reward (epr) and V(s_n) is given by the baselines.
def compute_n_step_targets(epr, baselines, gamma=0.999, n=15):
""" Computes a n_step target value. """
n_step_targets = np.zeros_like(epr)
## Code here
## target[t] = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + ... + \gamma^n V(s_{t+n})
for t_start in range(len(epr)):
# backward calculation
t_end = min(t_start+n,len(baselines)-1)
R = baselines[t_end]
for t in range(t_end-1, t_start-1, -1):
R = epr[t]+gamma*R
n_step_targets[t_start]=R
return n_step_targets
Actor-Critic n步Q值估计的性能
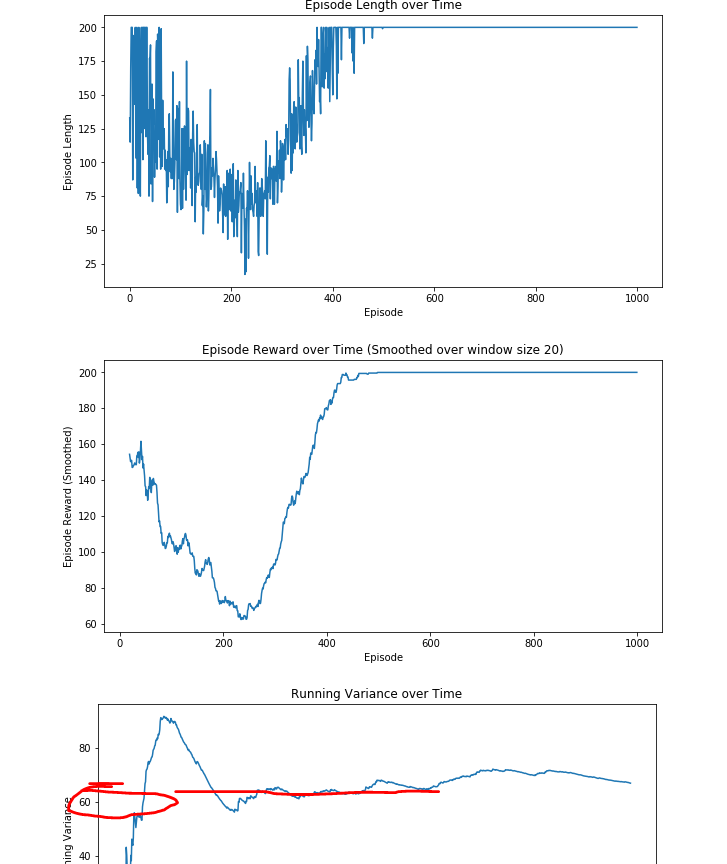
可以看出, 仍然需要500回合左右才能稳定得到运行200步的最大奖励, 但是方差进一步从带基线的REINFORCE算法的1000多降低到70左右
TRPO和PPO
在策略梯度算法中, 很多问题具有特征 1. reward稀疏, 2. target不固定,而是采样得到。在学习过程中容易“步子迈太大,容易扯着蛋”, 也就是学习的更新步长不好搞, 有个思路是用额外约束条件来限制策略更新, 使更新前后的策略不要相差太大.
TRPO直接约束: 更新前后两个策略的 KL 距离不超过一定阈值. 约束优化问题. 在TRPO中使使用拟牛顿法的conjugate gradient求近似解的,需要求KL divergence这个constraint的二次导.
PPO主要的改进是简化TRPO的优化方法. 避免求二次导, 直接把新旧策略的KL距离做在loss函数里.
对于优化问题, 一步到位的求解析解的优化, 无约束时一阶导数等于0求解, 等式约束时拉格朗日乘子法, 不等式约束时要用到KKT条件.
| 在监督学习中常见的带正则项的代价函数,例如lasso和ridge回归, 在原有的代价函数(例如回归问题时的最小均方差)上,在加上一阶或者二阶的惩罚项, $\lambda | w | $ . w为模型系数. 来达到既能优化最小均方差,同时又能满足某些条件. |
同理, 在策略梯度优化时, PPO额外加了一个惩罚项,其正比于新旧策略的KL距离.
PPO算法伪码

DPPO就是分布式的PPO
在Deepmind的DPPO文章中,除了用KL散度做额外的惩罚,也可以用clip的版本,据称效果更好.
参考
mircosoft course <<reinforcement learning explained>> on edx.org