无模型信息预测

说明

解决无模型预测和无模型控制的问题. 包含两个部分

策略评估 (policy evaluation)
策略控制 (policy control)

策略评估用于评估策略的好坏,而策略控制用来改进策略, 这里我们只讨论策略评估或者说是预测问题.

Model-free learning指我们将解决一个MDP(马尔科夫决策过程)问题,但是我们不知道控制该MDP的模型信息. 而在采用动态规划解决MDP问题时,我们是需要知道模型信息的,例如给定状态和动作,我们知道转移到新的不同状态的概率.

而解决model-free的学习问题，我们讨论

Monte Carlo learning
Temporal Difference Learning

符号

notations

State-value function 给出在服从策略$\pi$时状态s的真正价值. 从等式中看出是一个递归过程.

monte-carlo学习的策略评估

既然不知道马尔可夫过程的模型, 直接的想法就是做大量的实验, 从实验中进行统计和参数估计得到模型的估计. monte carlo学习就是这样的一个直接的解决方法

目标是从大量的实验回合中学习到在服从策略 $\pi$ 时的价值方程 $v_{pi}$ $S_1, A_1, R_2, ... S_k$
回报(return)为discounted的奖励的累积和 $G_t = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1}R_T$
价值方程为回报的期望
在MC学习中用实验(样本)均值来代替期望值

monte-carlo学习的策略评估的基本算法

服从策略 $\pi$ 的情况下采样出大量的回合实验
在回合中的每个时刻t时,当状态s出现时
- 计数器加一 $N(s) = N(s) + 1$
- 累积状态s的回报 $H(s) = H(s) + G_t$
- 用回报的均值估计价值 $V(s) = H(s)/N(s)$
根据大数定律有 $v(s) \rightarrow v_{\pi}(s)$ 当 $N(s) \rightarrow \infty$

增量更新方法

增量式的更新价值V
对于每个状态s,当其回报为 $G_t$ 有
- $N(s_t) = N(s_t) + 1$
- $V(s_t) = V(s_t) + \frac{1}{N(s_t)} (G_t - V(S_t))$

简单的增量公式推导, 为防止符号混淆, 记状态s在t时刻之前有价值V,累积回报G,累积访问计数N.

$V = \frac{G}{N}, V(s_t) = \frac{G+G_t(s)}{N+1}, N(s_t) = N + 1$

价值增量

$V(S_t) - V = \frac{N(G+G_t(s))-G(N+1)}{N(N+1)} = \frac{NG_t(s)-G}{N(N+1)} = \frac{G_t(s)}{N+1} - \frac{G}{N(N+1)} = \frac{G_t}{N_t} - \frac{V}{N_t}$

增量更新

$V(s_t) = V + \frac{1}{N_t}({G_t-V})$

更新系数

$\frac{1}{N_t}$

该系数为一个浮动系数, 随着t增大而减小. 当模型是变动时(例如状态a到状态b的转移概率随时间变化), 采用固定系数较好,通常用 $\alpha$ 表示

First-Visit 和 Every-Visit Monte-Carlo Policy Evaluation

First-Visit是指使用回报$G_t$估计状态价值时,t是第一次该状态被访问的时序步骤
First-Visit是指使用回报$G_t$估计状态价值时,t是每一次该状态被访问的时序步骤

first visit 方法

前面说的是每次访问状态s都累积求平均的做法,还有一种是在一个回合中只考虑首次访问状态的累积求和方法。

first visit MC

备注

monte-carlo学习的策略评估有一个问题, 那就是学习是要基于完整的回合. 因为更新需要用到回报 $G_t$. 只有当回合结束时才能计算得到

时序差分学习

简介

model free 学习
价值更新无需等待回合结束,使用bootstrapping
使用一个估计(历史的t+1的回报估计值)来更新另一个估计.

MC与TD的对比

MC and TD

从更新公式来看, TD是有偏估计因为V的估计用到了另一个估计量, 而MC是无偏估计,无偏估计量的期望等于真值.

样本的均值为无偏估计, 因为样本的均值的期望为真值 $\mu$.
而用样本均值 $\overline{X_i}$ 代替真值 $\mu$ 计算样本方差时为有偏估计.
TD使用了自助法(bootstrapping), 机器学习中bootstrapping指对数据集进行n次有放回的采样而形成的多个样本数据集进行模型训练,例如每个样本集会训练一个模型得到一个估计值，n个样本集会训练n个独立模型,最终的模型聚合了n个独立模型的输出,如随机森林,GDBT等等, 这里广义的指利用估计值进行估计的方法.

关于bootstrapping, 最常用的一种是.632自助法，假设给定的数据集包含d个样本。该数据集有放回地抽样d次，产生d个样本的训练集。这样原数据样本中的某些样本很可能在该样本集中出现多次。没有进入该训练集的样本最终形成检验集（测试集）。显然每个样本被选中的概率是1/d，因此未被选中的概率就是(1-1/d)，这样一个样本在训练集中没出现的概率就是d次都未被选中的概率，即 $(1-1/d)^d$ . 当d趋于无穷大时，这一概率就将趋近于e-1=0.368，所以留在训练集中的样本大概就占原来数据集的63.2%。

TD的例子

Driving Home Example

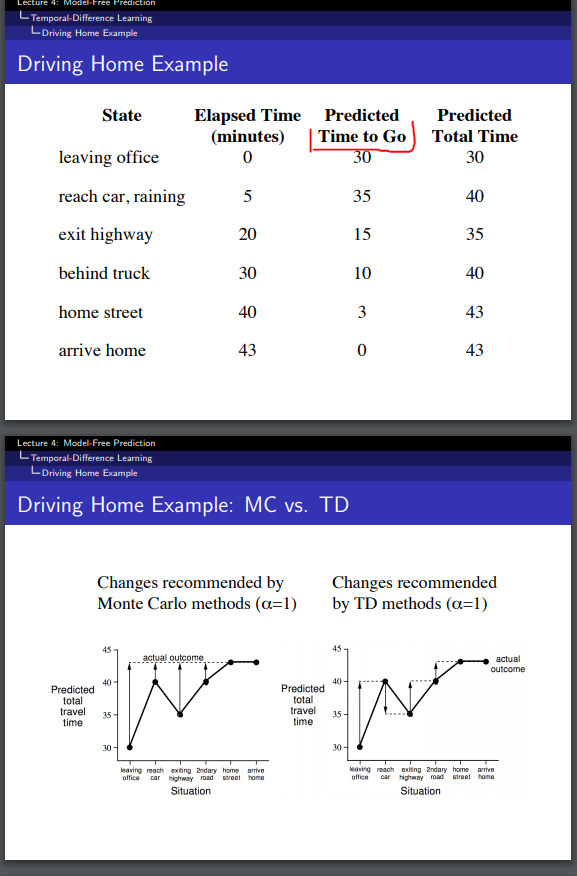
Driving Home

Predicted Time to Go ($V(S_t)$)是从历史回合中特出的估计值
当离开办公室时, 预估总时间为30
当到达汽车时,由于下雨, 预估剩余需要时间(类似 $V(S_{t+1})$), 改为35(来自历史经验), 而 $V(S_t)$ 更新为40, 此时TD error为 $G_t - V(S_t) = 43-40 = 3$
可以看出TD学习评估策略时,更新不必等到回合结束, 实际上在不断运用以前得到的估计值代替真实的回报
第二张图中更新的效果是一样的,但是MC是要等到到家后才进行更新的
实际运用中Predicted Time to Go可以是一个监督学习的时序预测,根据天气，不同道路，当前车流等等
这个例子中没有列出action供代理选择，譬如走高速还是不走高速等等.

这里我们利用下一步(时刻t+1)的估计值来更新当前的值, 这是一步时序差分记为TD(0). 而n步时序差分为TD($\lambda$)

收敛性, 对于任何固定的策略 $\pi$ , TD学习得到的v收敛到$v_\pi$

收敛速度比较, 采用MRP过程来对比MC和TD的收敛速度. MRP是没有action的MDP. 一个随机游走的MRP过程,如下图

Random Walk

由中间点C开始,每一步为50%向左或者向右, 移动到最左边或者最右边结束, 如果最右边结束则有奖励1, 其他情况奖励为0.

状态A到E,的真实价值为 $\frac{1}{6} \frac{2}{6} ... \frac{5}{6}$

结果如下

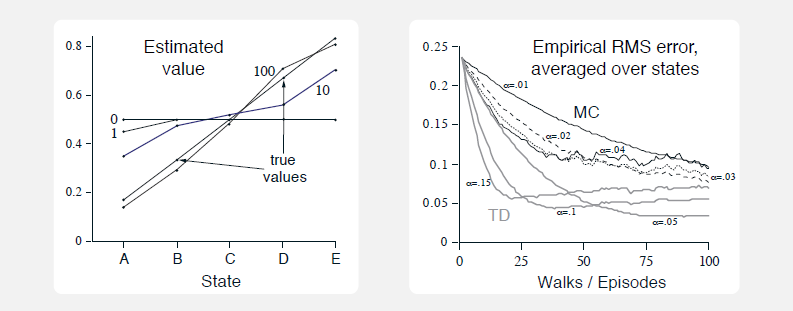
convergence

TD收敛快很多
有些TD曲线先下降而后略有上升只是由于最后一步的步长造成的, 一直运行下去的还是会稳定收敛的.

n步TD

上面提到的TD学习是利用t+1时刻状态价值的估计值来计算当前t时刻回报估计, 一种介于TD和MC学习之间的做法, 利用n步时刻之后(t+n)的回报估计来更新当前时刻(t)的状态价值估计. 当n趋于无穷时就是MC学习.

$n = 1, (TD), G_t^{(1)} = R_{t+1} + \gamma V(S_{t+1})$ $n = 2, (TD), G_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2V(S_{t+2})$ $...$ $n = \infty, (MC), G_t^{(\infty)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-t-1} R_T$

上式中T为最后一步的时刻, 我们有n步的回报定义为

$G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^n V(S_{t+n})$

n步TD学习的更新公式

$V(S_t) \leftarrow V(S_t) + \alpha (G_t^{(n)} - V(S_t))$

n步TD学习(预测问题)的例子, 19状态的随机游走, n=1 就是TD(0), 而n=512时就很接近MC学习. 在下面的例子中看出有时n取中间值例如4或者8时同时 $\alpha$ 为 0.2或者0.4好于两个极端值的情况

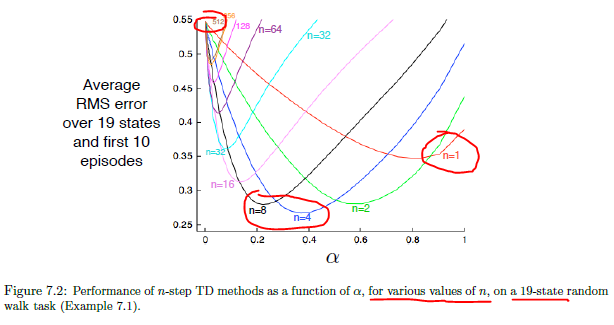
n step TD RandomWalk Comparation

TD $(\lambda)$

现在的问题是实际运用中如何选取n? 用n=4或者n=8来估计V,又或者把这两个估计的V平均一下. 既然想到了平均,那么是不是可以对不同n的估计值利用加权的方法进行融合一下呢? 这就是TD ($\lambda$) 的方法. 这种思路和卷积模型中的inception模型类似,既然卷积核的大小不好选,那就都选上然后加权和,不过inception的加权系数时学习到的,而不是等比.

如何设计加权的系数呢,

所有的权重系数和为1
各项系数间为等比数列. 就如同奖励随时间衰减一样.

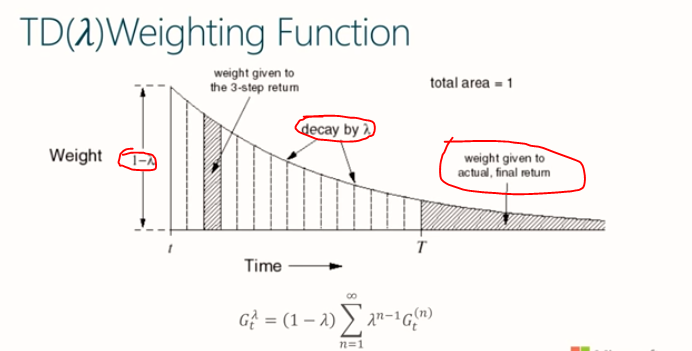
在TD($\lambda$) 中各项权重系数定义为 $(1-\lambda) \lambda^{n-1}$ 能满足上面的两个要求. 于是有回报的估计为

$G_t^{(\lambda)} = (1-\lambda) G_t^{(1)} + (1-\lambda) \lambda G_t^{(2)} ... + (1-\lambda) \lambda^{n-1} G_t^{(n)}$

备注, 实际上当n趋于无穷时所有系数和为1, 而在有限步后终止时, 所有系数之和不足1时的剩余部分都应该用作最终回报的系数. 其实可以想象在终止后仍然还有无穷多步,只不过每步都还停留在最终状态得到最终回报.

备注, $(1-\lambda)$ 实际上也就是归一化因子

备注, 设等比求和为1, 解方程可以得到首项为$(1-\lambda)$时能满足所有权重系数和为1

TD lambda weighting

前向视角

该视角也是 $TD(\lambda)$ 的定义, 需要用到将来直到回合终止时刻的回报加权和,

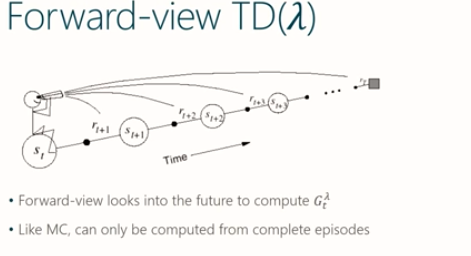
TD lambda forward view

更新公式

$V(S_t) \leftarrow V(S_t) + \alpha (G_t^{(\lambda)} - V(S_t))$

更新公式中用到lambda回报 $G_t^{(\lambda)}$ 作为目标, 其计算需要用到将来知道回合结束时每步的信息. 又回到MC的同样问题.

后向视角

顾名思义, 与其等待将来要发生的事情来更新当前, 不如记住过去的事情,用当前的状态来更新过去的状态值

从后往前,面朝已经经历过的状态流，获得当前回报并利用下一个状态的值函数得到TD偏差后，向已经经历过的状态通知，告诉这些已经经历过的状态处的值函数需要利用当前时刻的TD偏差进行更新。此时过往的每个状态值函数更新的大小应该跟距离当前状态的步数有关

前向视角提供了理论基础定义
后向视角提供了机制
在线更新, 从未完成的序列中每步更新

Eligibility Trace

当一系列的事件或者现象出现后，发生了某个特殊事件。那么最终的特殊事件的发生和前面一系列的事件和现象的关联是如何设定的?

credit assigment问题
频率相关，事件与其他事件或现象的次数相关，假设次数越多的越相关(其实应该考虑归一化后的频率比较)
发生时间相关，事件与其他事件的发生时间间隔相关，假设约近的越相关
Eligibility Trace 结合了发生频率和发生时间相关

$E_0(s) = 0$ $E_t(s) = \gamma \lambda E_{t-1}(s) + I(S==s)$

$I()$ 是指示函数,当函数内条件为真时值为1,否则为0

初始时所有状态的EligibilityTrace为0
t时刻的状态s的EligibilityTrace为衰减后的t-1时刻的EligibilityTrace, 若t时刻的状态 $s_t$ 为s则再加上1，否则就仅仅是衰减后的值

后向视角的更新机制

有了Eligibility Trace后可以定义后向更新机制如下, 在回合中的每个时刻t时

更新 $E_t(s) = \gamma \lambda E_{t-1}(s) + 1 (S==s)$
计算TD Error $\delta_t = R_{t+1}+\gamma V(S_{t+1}-V(S_t))$
使用Eligibility Trace作为Error的缩放因子来更新value function V(s). $V(s) \leftarrow V(s) - \alpha \delta_t E_t(s)$

We propagate current error information into the states we visited in the past. This allows us to combine the n-step returns in an online fashion

前向和后向视角对比

之所以单独一节，是因为这个对理解整个TD $(\lambda)$ 很有帮助。

前向视角是从定义来的, 对于t时刻的价值来说, 将来的每个时刻(包括t+1,t+2,…)的价值(及估计)都提供了有用的信息. 我们用加权和的方式来估计(确定)当前t时刻的价值。
后向视角便于计算和在线更新. 对于t时刻, 根据即时奖励和状态估计价值, 而估计出的价值对以前的每个时刻(t-1, t-2,…)的价值估计提供帮助. 采用Eligibility Trace的方式累积到以前的价值估计中去, 使以前时刻的价值估计包含都当前价值估计的信息.
前向后向视角的价值更新是一致的.这里就不推导公式了

参考

http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching_files/MC-TD.pdf http://www.cnblogs.com/jinxulin/p/3560737.html