无模型信息控制

说明

解决无模型预测和无模型控制的问题. 包含两个部分

策略评估 (policy evaluation)
策略控制 (policy control)

策略评估用于评估策略的好坏,而策略控制用来改进策略, 这里我们只讨论策略控制. 也就是结合策略评估提升策略的方法.

包含以下几个方面

On-policy Monte Carlo control
On-policy Temporal Difference control
Off-policy learning

On-policy 学习

“Learn on the job”
Learn about policy $\pi$ from experience sampled from $\pi$

简言之, 一边干一边学, 从自身的经验中学习.

Off-policy 学习

“Look over someone’s shoulder”
Learn about policy $\pi$ from experience sampled from $\mu$

简言之, 从别人的(服从其他策略的回合经验)中学习. 这种学习应当是离线的,不能一边干一边学.

直接的想法当然是Off-policy和On-policy结合使用啦.

通用的策略迭代框架

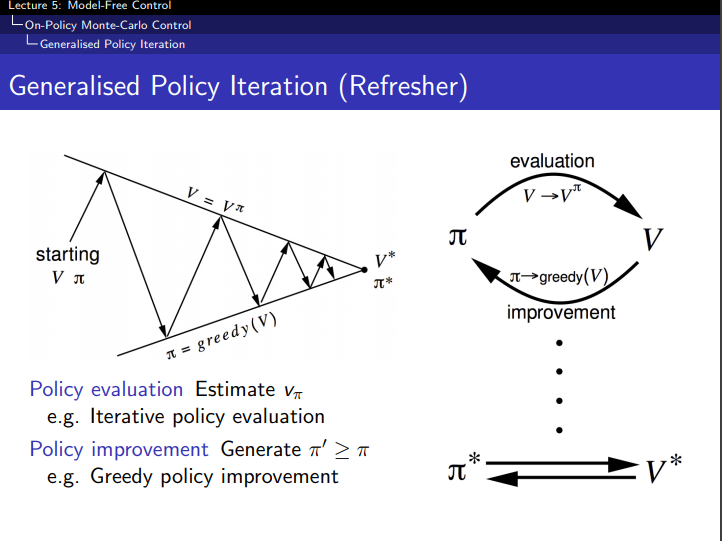
Generalised Policy Iteration

采用策略 $\pi$ 更新价值函数(例如通过采样)
利用更新的价值函数采用贪婪方法提升策略
反复更新价值函数和策略直至收敛

On-policy Monte Carlo control

价值函数

如果采用Greedy policy improvement,我们将使用什么价值函数来对策略进行评估?

采用状态-价值函数V(s), greedy policy improvement的更新 $\pi^\prime(s) = \mathop{\arg\max}_{a \in A} R_s^a + P_{ss^\prime}^aV(s^\prime)$
采用动作状态-价值函数Q(s,a), greedy policy improvement的更新 $\pi^\prime(s) = \mathop{\arg\max_{a \in A} Q(s, a)}$

价值函数将由策略评估来估计, 如果采用状态-价值函数的话，在策略控制中还需要一个执行动作a后的状态转移概率，这个信息是mdp模型信息，在无模型信息的策略控制中就还需要额外的过程来估计这个信息，所以不如直接使用动作状态-价值函数Q(s,a), 所以我们要学习的是Q价值函数, 而不是V价值函数.

$\epsilon$ -Greedy Exploration

增强学习的特有问题, exploration-exploitation-dilemma, 不能简单执行贪婪的算法，总是简单的选择最大收益的动作, 需要有一些机会来进行探索. 对贪婪算法最简单直接的改进

所有m个动作都需要有非零概率以便被尝试过
以概率 $(1-\epsilon)$ 选择贪婪动作, 即选取收益最大的动作exploitation
以概率 $\epsilon$ 选择去探索, 即以概率 )$\frac{\epsilon}{m}$ 随机选取动作

$\begin{equation} \pi(a \mid s) = \begin{cases} \epsilon / m + 1 - \epsilon & {if \space a^* = \mathop{\arg\max}_{a \in A} Q(s,a) }\\ \epsilon / m & \text{otherwise} \end{cases} \end{equation}$

$\epsilon$-Greedy Policy Improvement是确保新策略一定好于至少等于旧策略. 也就是保证策略是提升的.

下面的证明中需要指出对q取max一定大于任意的加权平均操作. 所以有

$\mathop{\max_{a \in A}}q_\pi(s,a) \ge \sum_{a \in A} \frac{\pi(a \mid s)-\epsilon/m}{1-\epsilon} q_\pi(s,a)$

于是

$q_\pi (s, \pi^\prime(s)) = \sum_{a \in A} \pi^\prime(a \mid s) q_{\pi}(s,a)$
$= \epsilon / m \sum_{a \in A} q_\pi(s,a) + (1-\epsilon) \mathop{\max_{a \in A}}q_\pi(s,a)$
$\ge \epsilon / m \sum_{a \in A} q_\pi(s,a) + (1-\epsilon) \sum_{a \in A} \frac{\pi(a \mid s)-\epsilon/m}{1-\epsilon} q_\pi(s,a)$
$= \sum_{a \in A} \pi(a \mid s)q_\pi(s,a) = v_\pi(s)$

思路是计算基于新策略选择动作后的价值函数要大于旧策略的价值函数. 价值函数分两个部分,一个部分是以概率 $\epsilon / m$ 探索,其产生的价值不会有差异. 第二个部分是根据策略选择已知最优动作而产生的价值.
直觉上很清楚，在经过可能发生的新的探索后, 对模型的信息有增益, 据此用贪婪算法选择的最优动作产生的价值会大于基于更少信息的旧策略的贪婪算法选择动作产生的价值

关于 $\epsilon$-Greedy 的策略提升方法, 实际上是要解决exploration-exploitation的难题, 如同摇臂赌博机问题一样，应该有对应的概率解法, 例如对离散的状态和动作，可以考虑用beta分布或者狄利克雷分布, 不断用先验概率和似然来计算后验概率, 执行少的动作方差大, 执行多的动作方差小, 可以选定最优动作的均值作为阀值, 用不同动作高于阈值的概率(概率密度函数的面积)比来进行动作的采样选择. 这种方法的缺点是需要假设分布函数. 同时如果价值函数随时间变化的话，就不如 $\epsilon$-Greedy 其一直会保持一定机会来随机探索.

Monte Carlo Control的策略迭代

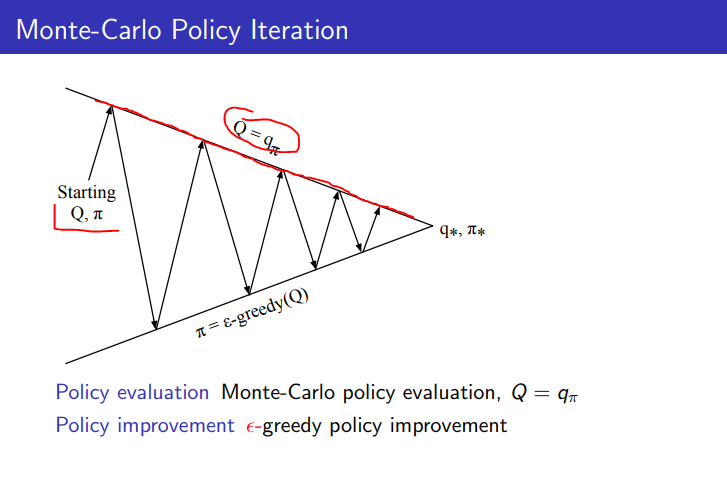
MC control policy iteration

由任意一个价值函数Q和策略 $\pi$ 开始
采用MC的方法, 即服从策略 $\pi$ 的条件下运行很多个回合, 来估计策略 $\pi$ 的动作状态-价值函数
在对策略估计完成后, 采用 $\epsilon$-greedy 策略提升的方法更新策略到 $\pi^\prime$
反复迭代直至收敛到贪婪算法下的最优价值函数和最优策略

缺点是效率低下

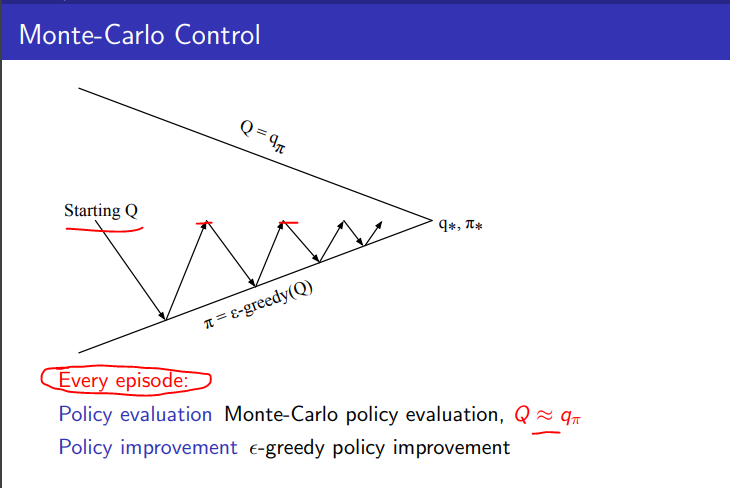
MC control policy iteration every episdo

一个直接的改进以提高效率的做法是在策略评估时,不是先执行多个回合然后评估一个准确的Q然后进行策略提升,而是在一个回合之后评估得到一个新的Q之后就立即进行策略提升. 有点类似Stochastic gradient descent的方式.

Greedy in the Limit with Infinite Exploration (GLIE)

目标

保证所有的状态都能被无限次的探索到
最后收敛到的最优策略中尽可能的不包含随机探索的部分

定义

所有的状态-动作对应当能无限多次的被尝试到 $\lim_{k \rightarrow \infty} N_k(s,a) = \infty$
策略应当收敛到一个贪婪策略 $\lim_{k \rightarrow \infty} \pi_k (a \mid s) = I(a= \mathop{\arg\max_{a^\prime \in A}} Q_k(s,a))$

对于 $\epsilon$-greddy来说就是需要 $\epsilon$ 不断减小(decay) 例如当 $\epsilon_k = \frac{1}{k}$ 时,随着k增大, $\epsilon$ 趋近于0, 此时的 $\epsilon-greedy$ 符合GLIE

GLIE Monte Carlo Control的策略迭代

使用策略 $\pi$, 进行第k个回合的采样
对于该回合中的每个状态 $S_t$ 和动作 $A_t$, 使用下面的方式更新状态动作-价值函数 Q
- 更新计数 $N(S_t, A_t) \leftarrow N(S_t,A_t) + 1$
- 更新Q函数均值，这里的均值不是普通意义上的均值，同时策略其实也一直在变. $Q(S_t, A_t) \leftarrow Q(S_t,A_t) + \frac{1}{N(S_t,A_t)}(G_t-Q(S_t,A_t))$
基于更新后的Q价值函数, 使用 $\epsilon-greedy$ 进行策略提升 $\epsilon \leftarrow 1/k$ $\pi \leftarrow \epsilon greedy(Q)$

实验，采用monte carlo control来玩21点

TD control

相对于mc,采用temporal difference方法来控制的优点

low variance
online
incomplete sequence

自然的想法, 在控制部分中采用TD来代替MC

Apply TD to Q(s,a)
Use $\epsilon$-greedy policy improvement
Update every time-step

SARSA

框架

由TD control导出的算法

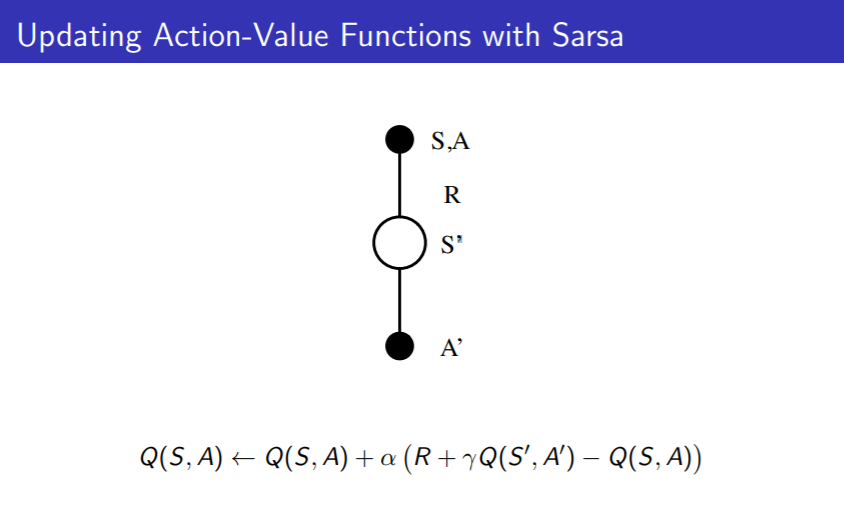
SARSA

SARSA的Q价值函数更新, 在原有的Q值 Q(S,A) 上, 朝着TD Target: R + $\gamma$Q(S’,A’) 移动一点点 $\alpha$

算法说明

将Policy Evaulation部分替换为SARSA的Q值更新过程, Policy Improvement采用 $\epsilon$-greedy 得到SARSA的On-Policy control算法

Initialize Q(s,a), $\forall s \in S, a \in A(s)$ , arbitrarily, and $Q(terminal-state, \cdot)=0$
Repeat (for each episdo)
- Initialize S
- Choose A from S using policy derived from Q (e.g. $\epsilon$-greedy)
- Repeat (for each step of episdo)
  - Take Action A, observe R, S’
  - Choose A’ from S’ using policy derived from Q (e.g. $\epsilon$-greedy)
  - $Q(S,A) \leftarrow Q(S,A) + \alpha (R+\gamma Q(S’,A’) - Q(S,A))$
  - $S \leftarrow S’, A \leftarrow A’$
- Until S is terminal

算法的中文说明

对于状态集合S和动作集合A中的所有状态动作对的Q(S,A)初始化为任意值, 并且设终止状态的Q值为0
对每个回合重复执行
- 初始化状态S为回合的初始状态
- 使用Q值根据策略从状态S中选取动作A, 如 $\epsilon$-greedy 方法
- 对回合中的每一步重复执行
  - 采取动作A, 并观察收获R和下一个状态S’
  - 使用Q值根据策略从状态S’中选取动作A’, 如 $\epsilon$-greedy 方法
  - $Q(S,A) \leftarrow Q(S,A) + \alpha (R+\gamma Q(S’,A’) - Q(S,A))$
  - $S \leftarrow S’, A \leftarrow A’$
- 直至状态S为终止状态

SARSA的收敛性

Q(S,A)收敛到 $q_*(s,a)$ 的条件

策略控制方法满足GLIE,例如 $\epsilon$不断衰减的 $\epsilon$-greedy,
每步的步长是robbins-monro序列, 也就是满足
- $\sum_{t=1}^{\infty} \alpha_t = \infty$
- $\sum_{t=1}^{\infty} \alpha_t^2 < \infty$

调和级数序列满足上面要求,也就是robbins-monro序列.

$\sum_{t=1}^{\infty} \frac{1}{t} = \infty$ $\sum_{t=1}^{\infty} \frac{1}{t^2} = \frac{\pi^2}{6}$

上述条件理论上保证收敛,实践中我们有时并不太关心收敛条件, SARSA基本都收敛.

SARSA的实验, Windy GridWorld

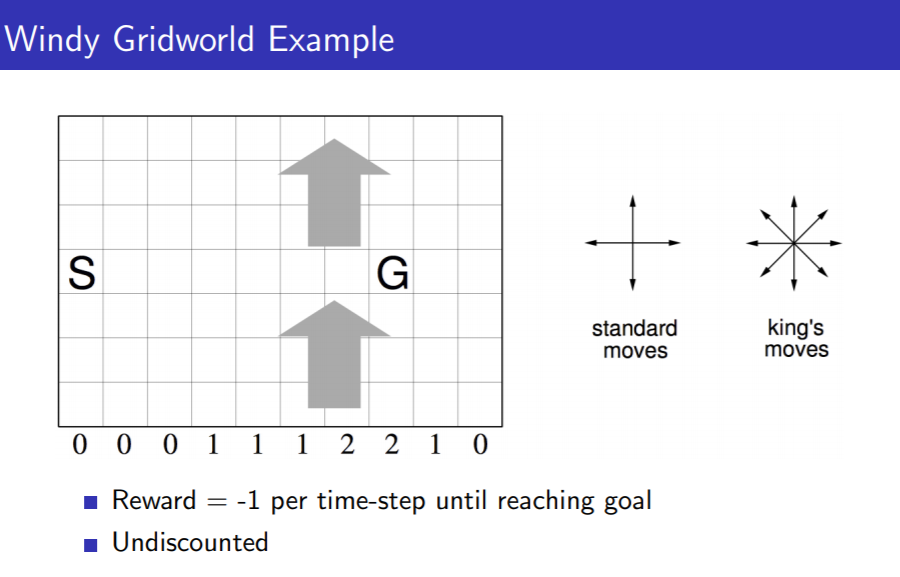
SARSA Example

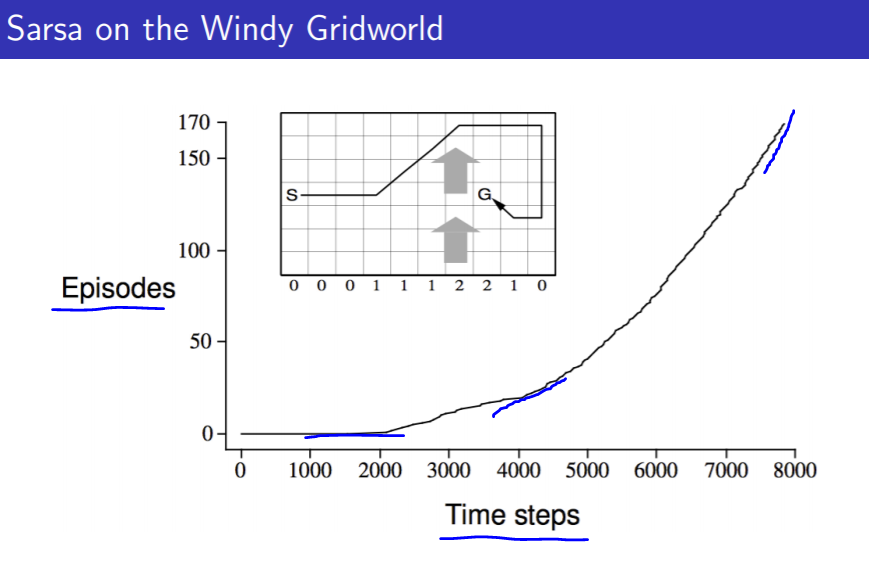
SARSA Example Result

在最开始的时候需要很多步才能完成很少的回合数,而到后面完成一个回合就不需要太多的步数了,从曲线的斜率变化就能看出

n-step SARSA

和上一章谈到的n-step TD类似, 这里给出n-step的Q值返回.

$n = 1, (SARSA), q_t^{(1)} = R_{t+1} + \gamma Q(S_{t+1})$ $n = 2, (SARSA), q_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2Q(S_{t+2})$ $...$ $n = \infty, (MC), q_t^{(\infty)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-t-1} R_T$

$q_t^{(n)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^n Q(S_{t+n})$

n-step Sarsa updates Q(s, a) towards the n-step Q-return

$Q(S,A) \leftarrow Q(S,A) + \alpha (q_t^{(n)} - Q(S,A))$

SARSA $\lambda$

前向视图

$q^\lambda$ return 是 $q_t^{(n)}$ 加权和
不同n的权重系数为
- $q_t^\lambda = (1-\lambda) \sum_{n=1}^\infty \lambda^{n-1} q_t^{(n)}$
前向视图的SARSA
- $Q(S,A) \leftarrow Q(S,A) + \alpha (q_t^{\lambda} - Q(S,A))$

同上一章的TD lambda算法,前向易于理解,但是在计算上要等到回合结束才能开始更新.

后向视图

使用eligibility trace的在线更新算法
对每个状态动作对,都需要eligibility trace
- $E_0(s,a) = 0$
- $E_t(s,a) = \gamma \lambda E_{t-1}(s,a) + 1(S_t=s, A_t=a)$
对每个状态s和动作a,Q(s,a)都需要更新
Q(s,a) update is in proportion to TD-error and eligibility trace
- $\delta_t=R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})-Q(S_t,A_t))$
- $Q(s,a) \leftarrow Q(s,a) + \alpha \delta_t E_t(s,a)$

思考,如何导出后向视图的更新公式?

算法说明

对于状态集合S和动作集合A中的所有状态动作对的Q(S,A)初始化为任意值
对每个回合重复执行
- 对于状态集合S和动作集合A中的所有状态动作对的E(S,A)=0
- 初始化状态S为回合的初始状态
- 使用Q值根据策略从状态S中选取动作A, 如 $\epsilon$-greedy 方法
- 对回合中的每一步重复执行
  - 采取动作A, 并观察返回R和下一个状态S’
  - 使用Q值根据策略从状态S’中选取动作A’, 如 $\epsilon$-greedy 方法
  - 计算error, $\delta \leftarrow R + \gamma Q(S’,A’) - Q(S,A)$
  - $E(S,A) \leftarrow E(S,A) + 1$
  - 对所有的 $s \in S, a \in A(s)$
    - $Q(s,a) \leftarrow Q(s,a)+\alpha \delta E(s,a)$
    - $E(s,a) \leftarrow \gamma E(s,a)$
  - $S \leftarrow S’, A \leftarrow A’$
- 直至状态S为终止状态

SARSA $\lambda$ 实验

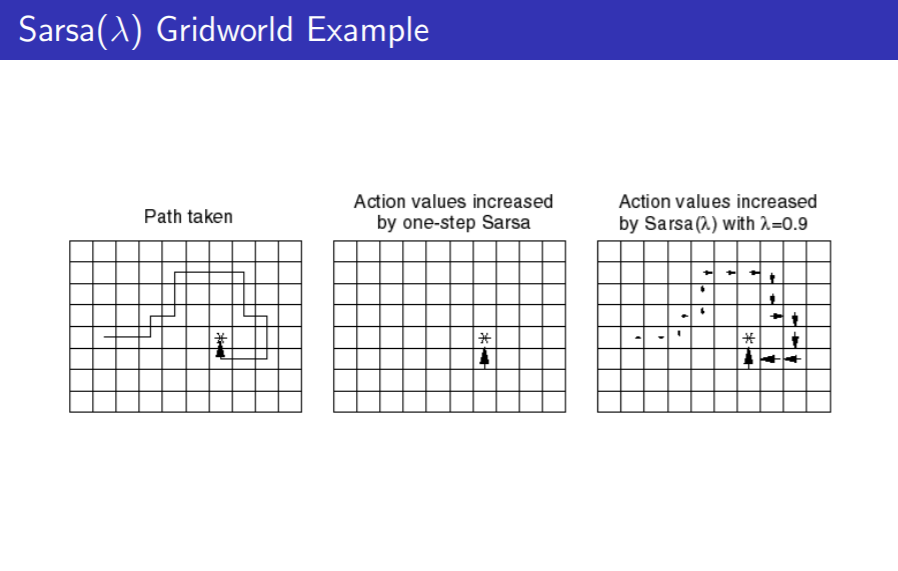
SARSA Lambda Example

与One-Step SARSA的区别在于,当回合结束是,路径上的所有状态都立即得到更新

off policy learning

目标策略, 待评估的策略
行为策略, 遵循的策略

利用待评估策略来估计Q值,然后生成自己的行为策略,然后服从行为策略执行动作. 有效利用别人的,或者是旧的策略所产生的经验.

off policy 的用途

从人类或者其他的代理学习
从旧的策略所获得的经验中学习
学习到最优策略(目标策略), 但是本身却需要服从具有探索性的策略. 具体见Q-learning
本身服从一个策略,但是需要学习多个不同的策略(的Q价值函数)

重要性采样

要解决off policy的问题有两个思路, 第一个方法是重要性采样

重要性采样可以利用一种分布进行采样,然后计算另一个分布相对的重要性权重,最后可以得到服从另一分布的期望.

$E_{X \sim P} [f(X)] = \sum P(X)f(X)$ $= \sum Q(X) \frac{P(X)}{Q(X)} f(X)$ $= E_{X \sim Q} [\frac{P(X)}{Q(X)} f (X)]$

采用重要性采样的off policy monte carlo

使用策略 $\mu$生成的返回(return)来评估策略 $\pi$
对返回 $G_t$ 根据策略间的相似性进行加权
对一个回合中需要计算多个重要性样本权重来对返回进行纠正 $G_t^{\pi/\mu} = \frac{\pi(A_t \mid S_t)}{\mu(A_t \mid S_t)} \frac{\pi(A_{t+1} \mid S_{t+1})}{\mu(A_{t+1} \mid S_{t+1})}...\frac{\pi(A_T \mid S_T)}{\mu(A_T \mid S_T)}$
用纠正后的返回来进行更新 $V(S_t) \leftarrow V(S_t) + \alpha(G^{\pi/\mu}-V(S_t))$
Cannot use if $\mu$ is zero when $\pi$ is non-zero
Importance sampling can dramatically increase variance

结论, 对于MC来说,不能采用重要性采样的方法

采用重要性采样的off policy TD

使用策略 $\mu$生成的TD target来评估策略 $\pi$
对TD target, $R + \gamma V(S’)$ 用重要性加权
仅需要对一步进行重要性纠正 $V(S_t) \leftarrow V(S_t) + \alpha (\frac{\pi(A_t \mid S_t)}{\mu(A_t \mid S_t)}(R_{t+1}+\gamma V(S_{t+1}))-V(S_t))$
Much lower variance than Monte-Carlo importance sampling
Policies only need to be similar over a single step

结论, 对于one step TD 来说,采用重要性采样的方法是可以的

Q-Learning

说明

On policy control的重要算法是SARSA,SARSA($\lambda$).
Off Policy control的重要算法是Q-Learning

特点

策略控制, 考虑的是评估状态动作价值函数Q(s,a)
无需重要性采样
下一个要执行的动作由行为策略给出, $A_{t+1} \sim \mu (\cdot \mid s_t)$
而利用下一步动作来尽心策略评估评估时(更新Q), 该动作是有目标策略给出的, $A \sim \pi(\cdot \mid s_t)$
更新 $Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1}, \color{red}{A^\prime}) - Q(S_t, A_t))$

注意, $A, A^\prime$ 是来自两个不同的策略

Off-Policy Control with Q-Learning

We now allow both behaviour and target policies to improve
The target policy $\pi$ is greedy w.r.t. Q(s, a) $\pi(S_{t+1}) = arg\max_{a\prime} Q(S_{t+1}, a^\prime)$
The behaviour policy $\mu$ is e.g. $\epsilon$-greedy w.r.t. Q(s, a)
The Q-learning target then simplifies: $R_{t+1} + \gamma Q(S_{t+1}, A^\prime)$ $= R_{t+1} + \gamma Q(S_{t+1}, \arg\max_{a^\prime} Q(S_{t+1}, a^\prime))$ $= R_{t+1} + \max_{a^\prime} \gamma Q(S_{t+1}, a^\prime)$

Q-Learning Vs One-step Sarsa

SARSA Q值的更新:

$Q(S,A) \leftarrow Q(S,A) + \alpha (R+\gamma Q(S',A') - Q(S,A))$

Q-Learning Q值的更新:

$Q(S,A) \leftarrow Q(S,A) + \alpha (R+ \gamma\max_{a^\prime} Q(S^\prime, a^\prime) - Q(S,A))$

One-Step SARSA算法

Initialize Q(s,a), $\forall s \in S, a \in A(s)$ , arbitrarily, and $Q(terminal-state, \cdot)=0$
Repeat (for each episdo)
- Initialize S
- Choose A from S using policy derived from Q (e.g. $\epsilon$-greedy)
- Repeat (for each step of episdo)
  - Take Action A, observe R, S’
  - Choose A’ from S’ using policy derived from Q (e.g. $\epsilon$-greedy)
  - $Q(S,A) \leftarrow Q(S,A) + \alpha (R+\gamma Q(S’,A’) - Q(S,A))$
  - $S \leftarrow S’, A \leftarrow A’$
- Until S is terminal

Q-Learning 算法

Initialize Q(s,a), $\forall s \in S, a \in A(s)$ , arbitrarily, and $Q(terminal-state, \cdot)=0$
Repeat (for each episdo)
- Initialize S
- Repeat (for each step of episdo)
  - Choose A from S using policy derived from Q (e.g. $\epsilon$-greedy) 动作由行为策略给出
  - Take Action A, observe R, S’
  - $Q(S,A) \leftarrow Q(S,A) + \alpha (R+ \gamma \max_{a^\prime} Q(S^\prime, a^\prime) - Q(S,A)$ 更新Q值时用的是目标策略(最优的贪婪策略)给出的动作
  - $S \leftarrow S’$
- Until S is terminal

Q-Learning 小结

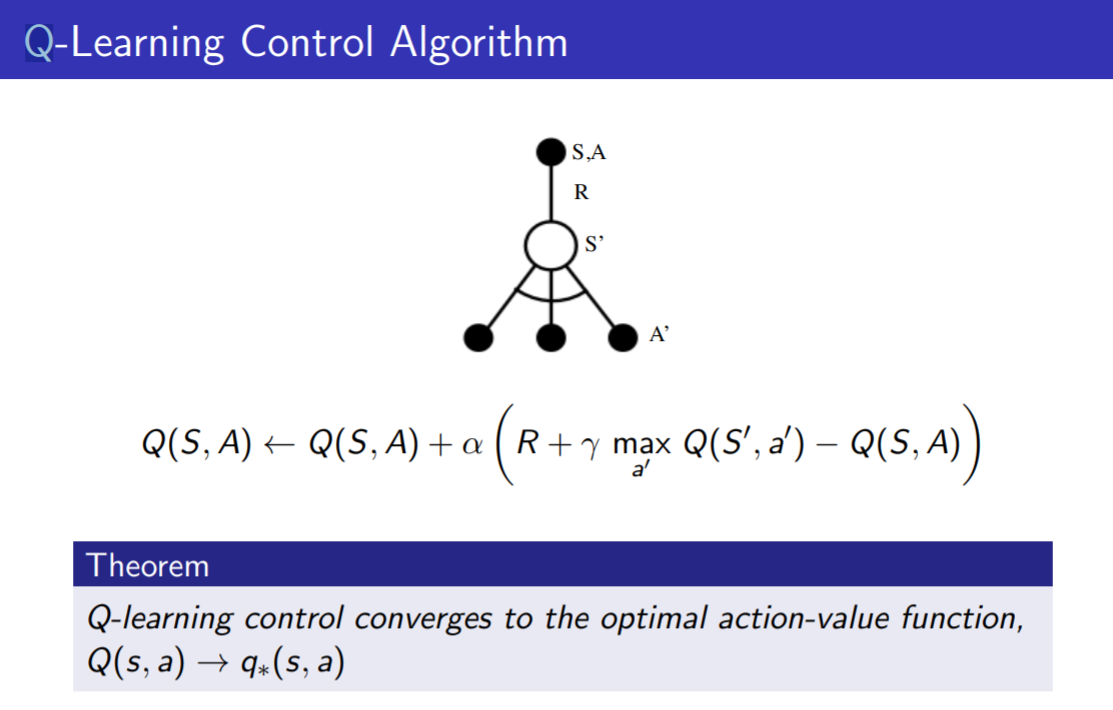
Q-Learning

在状态S,动作A的价值(Q值),是执行这一步所得到的即时奖励R,再加上打折后的下一步的状态S’和下一步根据状态由目标策略选出动作A’的Q值, Q(S’, A’).

在SARSA中目标策略和行为策略是同一个策略, 也就是 A,A’是由一个策略产生的, 而Q-Learning中目标策略和行为策略不是同一个策略.

参考

http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching_files/control.pdf