EM 算法简介

概述

EM算法的全称Expectation Maximization. 一般的引入从GMM开始,就高斯混合模型. 在高斯混合模型中,假设收集到一系列数据为符合多个高斯分布的随机变量$x$, 尽管我们可以知道随机变量$x$是来自n个高斯分布,n为已知. 但是我们不知道具体的某一个随机变量的样本如$x_i$是来自哪一个高斯分布,现在的问题是需要去估计这n个高斯分布的参数,也就是这n个高斯分布的均值和方差.

EM算法是一个贝叶斯网络的参数估计中重要算法. 注. HMM - Hidden Markov Model隐马尔可夫模型实际是贝叶斯网络的一个特例.

待优化的目标

从最大似然的思路出发,优化目标为给定n个高斯分布的参数,收集到的随机变量的样本出现的概率最大. 也就是最大化似然函数

$L(\theta) = argmax_\theta \prod_{i=1}^{m} {p(x_i\vert\theta)}$

m为样本总数, $\theta$ 为待优化的n个高斯分布的参数.

一般用最大似然方法, m个概率的连乘不够方便,所以最大化的是对数似然函数,两者问题是等价的. 也就是最大化 $log(\prod_{i=1}^{m} {p(x(i)\vert\theta)}) = \sum_i^m{log(p(x_i\vert\theta))}$

隐变量

在高斯混合模型问题中,有一个关键的变量我们缺失了,这就是随机变量的样本$x_i$是来自于那个高斯分布. 设一个隐变量$z$, $z_i$ 为样本点$x_i$来自于各高斯分布的概率.

于是待优化的目标就成为 $argmax_\theta \sum_i^m{log(\sum_zp(x_i,z_i\vert\theta))}$

思路

个人认为方法的发现是先有的直觉上的思路,然后在数学上推导出其合理性.

一般机器学习的方法是先给出一个带优化参数的假设值,多数情况都是随机给出假设值. 然后不断优化这个参数使代价函数不断减小.

同样的思路,我们可以随机给出$\theta$的假设值为起始值,设为$\theta_0$, 由$x_i$和$\theta_0$找出一个合理的$z_i$分布,直觉上,$z_i$的分布,我们设为$q_i(z_i)$就可以是给定$\theta_0$和$x_i$时$z_i$的概率分布,也就是$p(z_i \vert x_i,\theta_0)$, 再得到$z_i$的分布后,也就是样本点$x_i$来自于各高斯分布的概率已知,再用MLE(最大似然估计)优化而得到比$\theta_0$要估计的好的$\theta_1$. 反复迭代直至收敛.

每个迭代中分两步,称为E-Step, M-Step.

E-Step : 找出$z_i$的分布$q_i(z_i)$ M-Step : 用最大似然找出一个更好的参数估计值$\theta$

数学上的推导

待最大化的目标 $\sum_i^m{log(\sum_zp(x_i,z_i \vert \theta))}$ , 求和后取对数的函数是比较难优化的.

第一步，先引入$z_i$的概率分布,设为$q_i(z_i)$,该概率分布当前未知,但是是满足$\sum_z{q_i(z_i)}=1$, 也就是$z_i$来自于和高斯分布概率之和为1. 引入的方法为把待最大化目标改为 $\sum_i^m{log(\sum_z \frac{q_i(z_i) p(x_i,z_i\vert\theta)}{q_i(z_i)})}$ ,

修改后的目标函数仍然不好优化, 但是这个目标函数有一个下界,而且该下界是可以优化的.

使用Jensen不等式

Wiki Jensen不等式

简单说, 若函数$f(x)$为凸函数(开口向上),则有 $tf(x_1)+(1-t)f(x_2) >= f(tx_1+(1-t)x_2)$

下面是来自维基百科上的图片 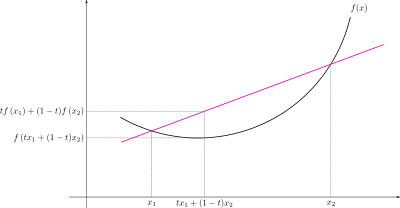Jensen Inequality

更一般的在概率上的表达为

如f为凸函数(开口向上),则有$f(E(x))<=E(f(x))$
如f为凹函数(开口向下),则有$f(E(x))>=E(f(x))$

log(x)中x取值>0,其的二阶导数为$-\frac{1}{x^2}<0$, log函数为凹函数. 根据jensen不等式 $\sum_i^m{log(\sum_z q_i(z_i) \frac{p(x_i,z_i\vert\theta)}{q_i(z_i)})} >= \sum_i^m{\sum_z q_i(z_i) log(\frac{p(x_i,z_i\vert\theta)}{q_i(z_i))})} $

找到了优化目标的下界函数, 不断调整$\theta$和隐变量分布$z_i$使下界函数最大化. 将上面的下界函数内的联合概率密度函数分解重写为 $\sum_i^m{\sum_z q_i(z_i) log(\frac{p(x_i,z_i\vert\theta)}{q_i(z_i))})}$
$ = \sum_i^m{\sum_z q_i(z_i)} log[p(x_i \vert \theta) \frac{p(z_i \vert x_i,\theta)}{q_i(z_i)}] $
$= \sum_i^m{\sum_z q_i(z_i)}(log(p(x_i \vert \theta)) + log(\frac{p(z_i \vert x_i,\theta)}{q_i(z_i)}) $ $= \sum_i^m{\sum_z q_i(z_i)}log(p(x_i \vert \theta)) + \sum_i^m{\sum_z q_i(z_i)}log(\frac{p(z_i \vert x_i,\theta)}{q_i(z_i)}) $

使用Gibbs不等式

从上一步的推导中,我们将待优化函数改为优化其下界函数,该下界函数有分解成两部分. 其中第二个部分中$\sum_z q_i(z_i)log(\frac{p(z_i \vert x_i,\theta)}{q_i(z_i)})$ 根据Gibbs不等式,其值小于等于0.

Gibbs 不等式如下

$ {-\sum_{i=1}^n p_i log(p_i)} <= {-\sum_{i=1}^n p_i log(q_i)} $

简而言之, 对任何概率分布p其信息熵小于等于p与另一个概率分布q的交叉熵. 其中等号在q于p相同时成立该不等式证明相当简单, 只需要用到$log(x)<=x-1$, 见Wiki Gibbs不等式

该不等式直接导出

$ 0 <= \sum_{i=1}^np_ilog(\frac{p_i}{q_i}) = D_{kl}(P \Vert Q) $ 也就是p和q的相对熵总是大于等于0
$ 0 >= \sum_{i=1}^np_ilog(\frac{q_i}{p_i})$ 也就是在我们的优化目标中第二项就有上界0。

回到我们优化目标的第二项,就有 $\sum_i^m{\sum_z q_i(z_i)}log(\frac{p(z_i \vert x_i,\theta)}{q_i(z_i)})<=0$, 当$q_i(z_i) = p(z_i \vert x_i,\theta)$时第二项得到最大值0. 这就是优化过程中E-Step的由来

设定$q_i(z_i) = p(z_i \vert x_i,\theta)$优化目标的第二项就为0, 在用MLE(最大似然估计),也就是$argmax_\theta \sum_i^m{\sum_z q_i(z_i)}log(p(x_i\vert\theta))$来估计出新的$\theta$. 这就是M-Step.

当新的$\theta$得到后第二项就又不为0,再重新做E-Step更新$q_i(z_i)$。

备注

网上常见的数学推导

网上常见的推导是指出,要使jensen不等式的等号成立,也就是下式成立 ${log(\sum_z q_i(z_i) \frac{p(x_i,z_i\vert\theta)}{q_i(z_i)})} == {\sum_z q_i(z_i) log(\frac{p(x_i,z_i\vert\theta)}{q_i(z_i))})} $

则需要$\frac{p(x_i,z_i\vert\theta)}{q_i(z_i))}$为常数,实际上是指与$z_i$无关, 显而易见,$p(x_i,z_i\vert\theta) = p(x_i\vert\theta)p(z_i \vert x_i,\theta)$, 这样当$q_i(z_i)=p(z_i \vert x_i,\theta)$时，$\frac{p(x_i,z_i \vert \theta)}{q_i(z_i))}$就与$z_i$无关.

同时, Gibbs不等式也可以从Jensen不等式直接导出.

关于参数的说明

E-Step 导出的是$z_i$的分布,对于GMM来说就是一个n维的向量,和为1。参数$\theta$对于GMM来说是一个均值的向量和一个协方差矩阵.