二项分布,负二项分布简介

二项分布

对于经典的抛硬币的实验,给定$\theta$为抛硬币正面向上的概率关于在n次实验中出现正面向上的次数为k次的二项分布的概率质量函数为

$p(k \vert n,\theta) = \dbinom{n}{k} \theta^k (1-\theta)^{(n-k)} = \frac{n!}{k!(n-k)!} \theta^k (1-\theta)^{(n-k)}$

简单的理解就是n次实验中发生k次正面向上的情况一共有(n选k)种组合. 每中组合发生的概率为$\theta^k (1-\theta)^{(n-k)}$

下图为10次实验正面向上为5次的概率质量函数 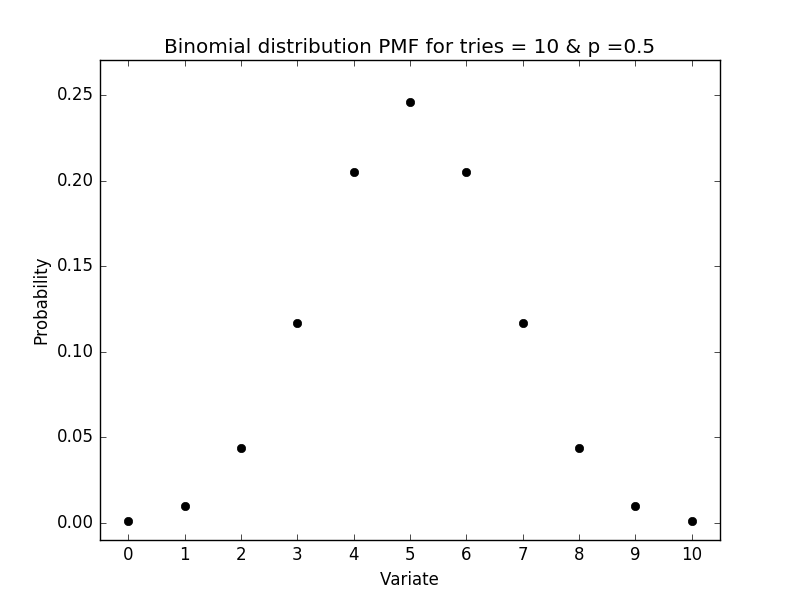binomial pmf

“负二项分布”与“二项分布”的区别在于：“二项分布”是固定试验总次数N的独立试验中，成功次数k的分布；而“负二项分布”是所有到成功r次时即终止的独立试验中，失败次数k的分布。

由于成功r次时即终止,所以第r次必为成功在前r+k-1次实验中出现r-1次成功,k次失败服从二项分布由此可得

$p(k \vert n,\theta) = \dbinom{r+k-1}{r-1} \theta^{r-1} (1-\theta)^{k} \theta = \frac{(r+k-1)!}{k!(r-1)!} \theta^{r} (1-\theta)^{k}$

当r=1时,负二项分布退化为几何分布