beta分布,dirichlet分布与贝叶斯参数估计简介

概述

最大似然估计与最大后验估计

最大似然估计也就是最大化似然函数

$L(\theta) = argmax_\theta {p(x \vert \theta)}$

最大后验估计也就是最大化后验概率

$\hat{\theta}_{MAP}(x) = argmax_\theta f(x \vert \theta)g(\theta)$

$g(\theta)$ 为参数 $\theta$ 的先验概率分布

相比于最大似然估计,最大后验估计考虑了参数本身也是一个随机变量,在估计时使用了参数的先验概率分布. 从机器学习的角度来看, 最大后验概率估计可以看作是规则化(regularization)的最大似然估计。

从wiki上关于map的介绍, 最大后验估计(贝叶斯估计)的计算方法有下列几种

解析方法，当后验分布的模能够用闭合形式方式表示的时候用这种方法.当使用共轭先验的时候就是这种情况.
通过如共扼积分法或者牛顿法这样的数值优化方法进行,这通常需要一阶或者导数,导数需要通过解析或者数值方法得到.
通过期望最大化(EM)算法的修改实现,这种方法不需要后验密度的导数.

本文讨论离散情况下,使用共轭先验概率的贝叶斯估计

二项分布与Beta分布

二项分布

对于经典的抛硬币的实验,给定$\theta$为抛硬币正面向上的概率关于在n次实验中出现正面向上的次数为k次的二项分布的概率质量函数为

$p(k \vert n,\theta) = \dbinom{n}{k} \theta^k (1-\theta)^{(n-k)} = \frac{n!}{k!(n-k)!} \theta^k (1-\theta)^{(n-k)}$

下图为10次实验正面向上为5次的概率质量函数 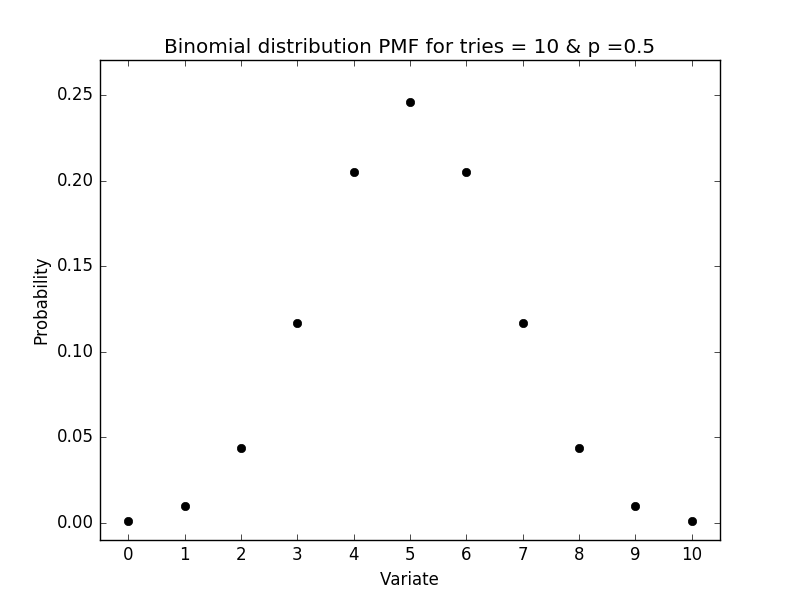binomial pmf

共轭先验分布

假设我们做了10次实验,出现7次正面向上.

对于最大似然估计只需要要将n=10, k=7代入二项分布的概率质量函数,然后取对数,求一阶导数并设为0可以求得$\theta = 0.7$

而对于采用共轭先验的贝叶斯估计,我们则需要给出二项分布的参数的先验分布.对于上述抛硬币的实验,(个人认为)先验分布应当具有下列特性

当我们对事物一无所知时先验分布可以转变成均匀分布
后续的实验可以方便利用已做实验的结果. 例如后续又继续做10次实验并得到正面向上的次数为8次, 本质上不应当是认为$\theta=0.8$, 在序列模型中应当考虑到前面实验的结果, 对于最大后验估计来说要得到这种便利性, 实际上是将上次实验得到的后验估计可以作为下次实验的先验. 这就需要保持后验分布与先验分布是同一种分布.
当实验次数趋于无穷大时先验分布就应当逼近真实概率的分布, 在抛硬币实验中,其实是趋于真实的正面向上的概率分布,也就是真实概率的二项分布

对于共轭先验的wiki上的定义: 在贝叶斯统计中，如果后验分布与先验分布属于同类，则先验分布与后验分布被称为共轭分布. 高斯分布家族在高斯似然函数下与其自身共轭

那么对于二项分布似然函数的共轭分布是什么分布呢? Beta 分布

Beta 分布

Beta分布的定义如下

$Beta(\theta \vert \alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \theta^{\alpha-1}(1-\theta)^{\beta-1} = \frac{1}{B(\alpha,\beta)} \theta^{\alpha-1} (1-\theta)^{\beta-1}$

上面的公式用到了Gamma函数和Beta函数

Gamma 函数

$\Gamma(x) = \int_{0}^{\infty} t^{x-1} e^{-t} dt$

Gamma的介绍可以参考网上的文章, http://cos.name/2013/01/lda-math-gamma-function/, 快速的理解可以直接认为是阶乘在实数和复数域的推广. Gamma函数具有下列性质

$\Gamma(x+1) = x\Gamma(x)$ $\Gamma(x) = (n-1)!$

Beta 函数

$B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$

同时

$B(\alpha,\beta) = \int_{0}^1 t^{\alpha-1}(1-t)^{\beta-1}dt$

Beta 分布与二项分布的比较

用$\alpha = k, \beta = n-k$代入Beta分布的公式,由于$\alpha,\beta$都被限制在整数,用阶乘的方式来表示Gamma函数

$\begin{aligned} Beta(\theta \vert \alpha,\beta) = \frac{\Gamma(k+n-k)}{\Gamma(k)\Gamma(n-k)} \theta^{k-1}(1-\theta)^{n-k-1} \\ = \frac{(n-1)!}{(k-1)!(n-k-1)!} \theta^k (1-\theta)^{n-k} \frac{1}{\theta (1-\theta)} \\ = \frac{n!}{k!(n-k)!} \theta^k (1-\theta)^{n-k} \frac{k(n-k)}{n} \frac{1}{\theta (1-\theta)} \end{aligned}$

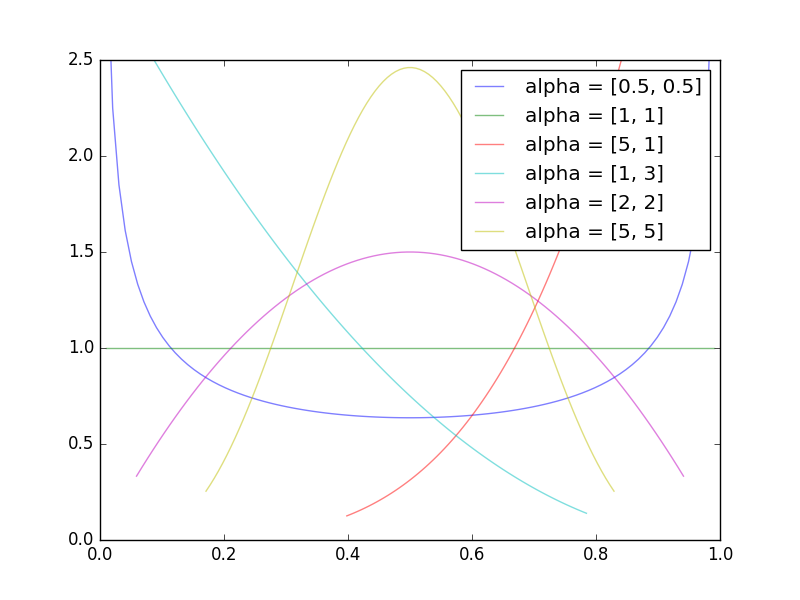
可以看出Beta分布与二项分布的差异,当取$\alpha = k, \beta = n-k $时beta分布为二项分布乘以系数项$\frac{k(n-k)}{n} \frac{1}{\theta (1-\theta)} $ 当$\alpha, \beta$取值较大时,$\frac{k}{n} \approx \theta, \frac{n-k}{n} \approx (1-\theta)$,beta分布就逼近真实概率下的二项分布. 当$\alpha,\beta$取值较小时,如(1,1),Beta分布为均匀分布

下图为beta分布的pdf

beta pdf

基于二项分布与beta先验分布的贝叶斯估计

在进行n次试验,并发生k次正面向上的抛硬币的后,关于正面向上的后验概率为

$p(\theta \vert D) = \frac{p(D \vert \theta) p(\theta)}{p(D)}$

D 为实验后数据即n次试验k次正面向上

似然函数为二项分布 $p(D \vert \theta) = \dbinom{n}{k} \theta^k (1-\theta)^{(n-k)} $ 先验概率为beta分布 $p(\theta) = \frac{1}{B(\alpha,\beta)} \theta^{\alpha-1} (1-\theta)^{\beta-1} $

上式中分子部分为

$\begin{aligned} p(D \vert \theta) p(\theta) = \dbinom{n}{k} \theta^k (1-\theta)^{(n-k)} \frac{1}{B(\alpha,\beta)} \theta^{\alpha-1} (1-\theta)^{\beta-1} \\ = \dbinom{n}{k} \frac{1}{B(\alpha,\beta)} \theta^{\alpha+k-1} (1-\theta)^{\beta+n-k-1} \end{aligned}$

归一化因子为

$\begin{aligned} p(D) = \int_0^1 p(D \vert \theta)p(\theta)d\theta \\ = \int_0^1 \dbinom{n}{k} \frac{1}{B(\alpha,\beta)} \theta^{\alpha+k-1} (1-\theta)^{\beta+n-k-1} d\theta \\ = \dbinom{n}{k} \frac{1}{B(\alpha,\beta)} \int_0^1 \theta^{\alpha+k-1} (1-\theta)^{\beta+n-k-1} d\theta = \dbinom{n}{k} \frac{1}{B(\alpha,\beta)} B(\alpha+k,\beta+n-k) \end{aligned}$

回顾前面关于Beta函数的定义

$B(\alpha,\beta) = \int_{0}^1 t^{\alpha-1}(1-t)^{\beta-1}dt$

最后的后验概率为

$p(\theta \vert D) = \frac{p(D \vert \theta) p(\theta)}{p(D)} = \frac{1}{B(\alpha+k,\beta+n-k)} \theta^{\alpha+k-1} (1-\theta)^{\beta+n-k-1}$

后验概率仍是一个Beta分布$Beta(\theta \vert \alpha+k,\beta+n-k)$, 可以作为下一次实验估计用的先验概率

多项分布与Dirichlet分布

多项分布

当实验结果可能有k种取值时,二项分布要扩展成多项分布. 例如掷骰子游戏

对于n次实验,试验结果可能有k种取值,$\theta_i$为第i种取值发生的概率, 记$x_i$为第i种取值发生的次数, 多项分布的概率质量函数为

$p(x_1,...x_k \vert n, \theta_1, ... \theta_k) = \frac{n!}{x_1!...x_k!} \theta_1^{x_1}...\theta_k^{x_k}$

可以看出多项分布就是二项分布的扩展.

Dirichlet 分布

Dirichlet分布就是多项分布对应共轭分布. 在贝叶斯参数估计中,用作多项分布的先验概率

Beta分布的超参有两个$\alpha,\beta$, 而Dirichlet分布的超参则有k个,对应多项分布的k种取值,记为$\alpha = (\alpha_1, … \alpha_k)$

$p(\theta_1,...,\theta_k) = \frac{1}{Beta(\alpha)} \prod_{i=1}^k \theta_i^{\alpha_i-1}$ $Beta(\alpha) = \frac{\prod_{i=1}^k \Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^k \alpha_i)}$

可以看出Dirichlet分布就是Beta分布的扩展.

基于多项分布与Dirichlet先验分布的贝叶斯估计

对于n次实验,试验结果可能有k种取值,记$x_i$为第i种取值发生的次数, 采用超参为$\alpha=(\alpha_1,…,\alpha_k)$的Dirichlet分布为参数$\theta = (\theta_1, … \theta_k)$先验概率分布, 其后验概率如下

$p(\theta \vert D) = \frac{\Gamma(\sum_{i=1}^k \alpha_i + n)}{\prod_{i=1}^k \Gamma(\alpha_i+x_i)} \prod_{i=1}^k \theta_i^{\alpha_i+x_i-1} = \frac{1}{Beta(\alpha^\prime)} \prod_{i=1}^k \theta_i^{\alpha_i^\prime-1}$

其中$\alpha^\prime = (\alpha_1^\prime,…, \alpha_k^\prime) = (\alpha_1+x_1, …, \alpha_k+x_k) $

推导过程类似于二项分布时,用Beta分布做先验分布求后验概率. 此处略去.

总结

Beta分布为似然函数为二项分布的共轭先验分布
Dirichlet为似然函数为多项分布的共轭先验分布,是Beta分布的推广
Dirichlet的超参为$\alpha = (\alpha_1,…,\alpha_k)$, 参数的个数k为对应多项分布中单次实验可取值的个数.同时,估计参数$\theta=(\theta_1,…,\theta_k)$也为k个
Dirichlet中的$Beta(\alpha)$实际为对于参数$\theta$的归一化因子.
Dirichlet分布超参$\alpha$的值的大小对应先验的强度,相互比值对应先验估计的概率值，例如Diri(1,1)表明先验对两种取值概率的估计为(0.5,0.5),但是这是很弱的先验,其概率密度函数为均匀分布,而Diri(30,30)仍然标明对两种取值概率的估计为(0.5,0.5),但这个先验分布是比较强的,其概率密度函数接近多项(二项)分布,形状为比较尖锐的钟形